【高校数A】整数の性質「素数と素因数分解」を元数学科が解説

前回に引き続き整数の性質についての記事になります。

 

 

『素数』とは？

まずは素数について、そもそも素数とはなんぞや？？

ズバリ素数とは

１とその数自身以外に正の約数を持たない数

のことです。

約数について分からない方は、前回の記事にまとめてありますので良かったらご覧ください。

 

「素因数分解」について

さて本題の素因数分解について勉強する前に「因数」「素因数」について理解しましょう。

「因数」について

例えば”72″について

$72=3 \times 24$
$72=2 \times 3 \times 12$
…

みたいに１つの数に対していくつかの掛け算のパターンで表せますね？

このように１つの数をいくつかの掛け算に分解するのを因数分解と言います。

例えば

$x^2+9x+18=(x+6)(x+3)$

これは「$x^2+9x+18$」を
$(x+6) \times (x+3)$
という掛け算に分解しているんですね(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

 

実際に素因数分解をやってみよう！

いよいよ本日のメイン『素因数分解』を解説します！

素因数分解とは

素数のみの因数分解

です。

例えば”72″なんかは

$72=3 \times 24$
$72=2 \times 3 \times 8$
…

など因数分解できます。パターンを全て出してみましょう。

$72=2 \times 36$
$72=2 \times 2 \times 18$
$72=2 \times 2 \times 2 \times 9$
$72=2 \times 2 \times 2 \times 3 \times 3$

これを「因数分解」「素因数分解」に分けます。

素因数分解の計算方法

先ほど例に出した”72″はそんなに大きい数字ではないので簡単に素因数分解できますが、もっと大きな数字を素因数分解する時はこうはいきません。

こんな時に使える素因数分解の計算方法をお伝えします(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

を使います。

 

例えば”882″を素因数分解してみましょう！

①素因数分解する数字を一番上に書く

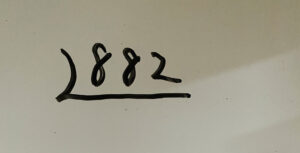
ほいこんな感じ！

②割り切れる数字を左に書く

例えば882は偶数なので素因数2で割り切れますね？なので

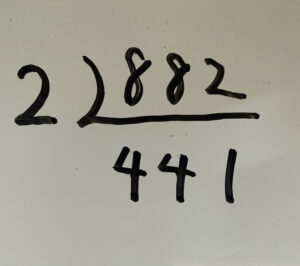
こう書けます。下には割った商を書きます。

これを、商が素因数になるまで続けます。

【高校数A】整数の性質「約数と倍数」「倍数の判定法」を元数学科が解説

今回は【高校数学】【数A】『整数の性質』から「約数と倍数」「倍数の判定方法」を解説しました。教科書だと３、４ページくらいで収まる内容を丁寧に解説してみましたので、数学が苦手な方はぜひご覧ください！約数、倍数の定義や倍数の判定方法の証明などなど…

www.zilleblog.com

2022.02.11

 

では実際に素因数分解してみましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

以上から

$882=2 \times 3^2 \times 7^2$

 

頻出問題を解説

問題１：$\sqrt{480n}$が自然数になる最小の自然数nを求めなさい。

例えば

$\sqrt{9} =\sqrt{3^2} =3$
$\sqrt{64} =\sqrt{8^2}=8$

みたいなね！

 

では手順を追ってじっくり丁寧に解説します( ^ω^ )

 

手順❶：$\sqrt{◯n}$の◯を素因数分解する

480を素因数分解してみましょう。

よって

$480=2^5 \times 3 \times 5$

 

手順❷：❶に何を掛ければ２乗になるか考える

$480=2^5 \times 3 \times 5 \times n=○^2$

を満たす最小のnを考えましょう。

 

ここで注目して欲しいのが

$2^4=(2^2)^2=4^2$
$3^6=(3^3)^2=27^2$

つまり

$○^{2x} =(○^x)^2$

が成立するってことです( ^ω^ )

さらに

$(2^2 \times 3^2)=(2 \times 3)^2=6^2$
$2^4 \times 3^6=(2^2 \times 3^3)^2=108^2$

も成立します。

以上から次に考えるのは

$480=2^5 \times 3 \times 5$
の各因数$2^5,3,5$の指数を偶数になるように調整する。

ことです。

 

 

・$2^5$の指数
指数は5は奇数より、2をもう１つ掛けて
$2^5 \times 2=2^6$
と調整します。

・3の指数
$3=3^1$であってつまり指数は１で奇数なので、3をもう１つ掛けて
$3 \times 3=3^2$
と調整します。

・5の指数
$5=5^1$であってつまり指数は１で奇数なので、5をもう１つ掛けて
$5 \times 5=5^2$
と調整します。

つまりですね

$480=2^5 \times 3 \times 5$について

$(2^5 \times 3 \times 5) \times (2 \times 3 \times 5)=2^6 \times 3^2 \times 5^2$
$=(2^3 \times 3 \times 5)^2$

が成立します(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾

したがって

$n=2 \times 3 \times 5=30$

答えは$n=30$

 

問題２：$\sqrt{\frac{600}{n}}$が自然数になるような最小の自然数nを求めなさい。

 

 

手順❶：$\sqrt{\frac{○}{n}}$の○部分を素因数分解する。

600を素因数分解してみましょう。

つまり$600=2^3 \times 3 \times 5^2$

 

手順❷：❶の数に何を割れば２乗になるか考える。

$600=2^3 \times 3 \times 5^2$

各因数について

・$2^3$の指数
指数は3で奇数なので、2で割って偶数になるように調整しましょう。
$2^3 \div 2=2^2$

・3の指数
指数は1で奇数なので、3で割って偶数になるように調整しましょう。
$3 \div 3=1=3^0$

・$5^2$の指数
指数は2で偶数なのでそのままでオッケー。

 

つまり$600=2^3 \times 3 \times 5^2$について

$\frac{600}{2 \times 3}=\frac{2^3 \times 3 \times 5^2}{2 \times 3}=2^2 \times 5^2=100=10^2$

したがって$n=2 \times 3=6$

答えは$n=6$。

 

最後に