
みなさんおはこんばんにちは。
年末大掃除したにも関わらずもう部屋が散らかっているジルでございます!
今回は前回の「三角比」における重要公式の解説に続いた内容を解説します。
今まで学んできた三角形の$θ$は$0° \leqq θ \leqq 90°$の場合でしたね?
今記事ではもう少し範囲を拡張して$0° \leqq θ \leqq 180°$で考えていきます。
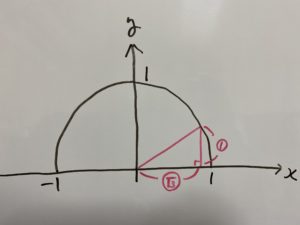
$xy$座標を用います。
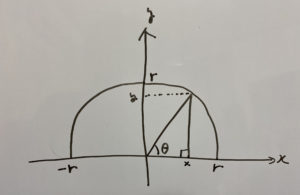
画像のように斜辺が$r$の三角形ができるケースを考えます。
この時
$\sin θ=\frac{y}{r}$、$\cos θ=\frac{x}{r}$、$\tan θ=\frac{y}{x}$
この$xy$座標を見てもらうと$x,y$の取りうる範囲は
$-r \leqq x \leqq r$、$0 \leqq y \leqq r$
となります。
ここで見ていただきたいのは$90° \leqq θ \leqq 180°$の場合です。
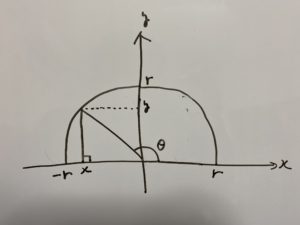
この時できる三角形を切り取ってみると
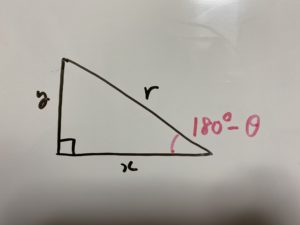
このようになります。なので
$\sin (180°-θ)$、$\cos (180°-θ)$、$\tan (180°-θ)$
を考える必要がありますね?
ここで今回覚えてもらう公式を出します。
$\sin (180°-θ)=\sin θ$
$\cos (180°-θ)=-\cos θ$
$\tan (180°-θ)=-\tan θ$
こちら!覚えてね!

$\sin (90°-θ)=\cos θ$
$\cos (90°-θ)=\sin θ$
$\tan (90°-θ)=\frac{1}{\tan θ}$
も併せて今度解説記事を書こうかなと考えております(*´∀`*)
また、$0° \leqq θ \leqq 180°$に拡張した場合でも
$\sin θ=\cos θ \times \tan θ$
$\sin^2 θ + \cos^2 θ =1$
$1+\tan^2 θ =\frac{1}{\cos^2 θ}$
は成立します。
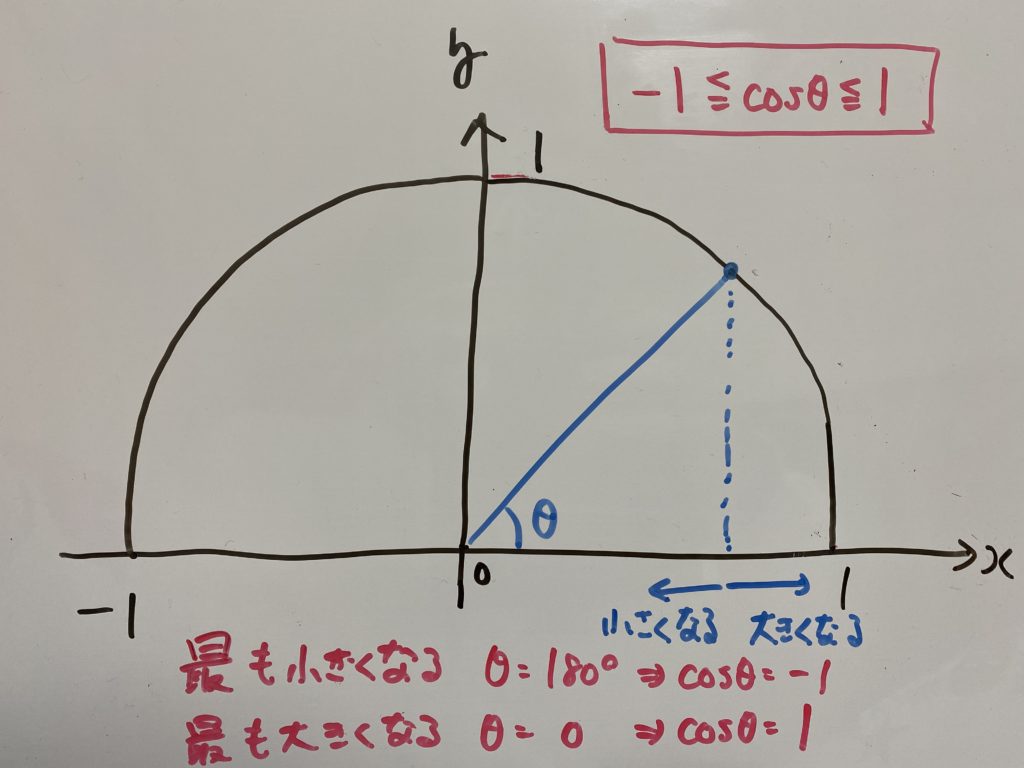
$θ$によって$\sin θ$、$\cos θ$、$\tan θ$はどう変わっていくか
ここで$0 \leqq θ \leqq 180°$における$\sin θ$、$\cos θ$、$\tan θ$の移り変わりを確認しましょう。
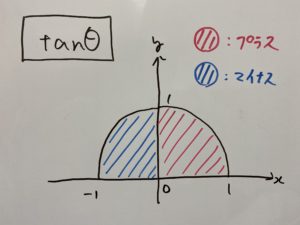
$\sin θ$は$θ$によってどう変わるか?
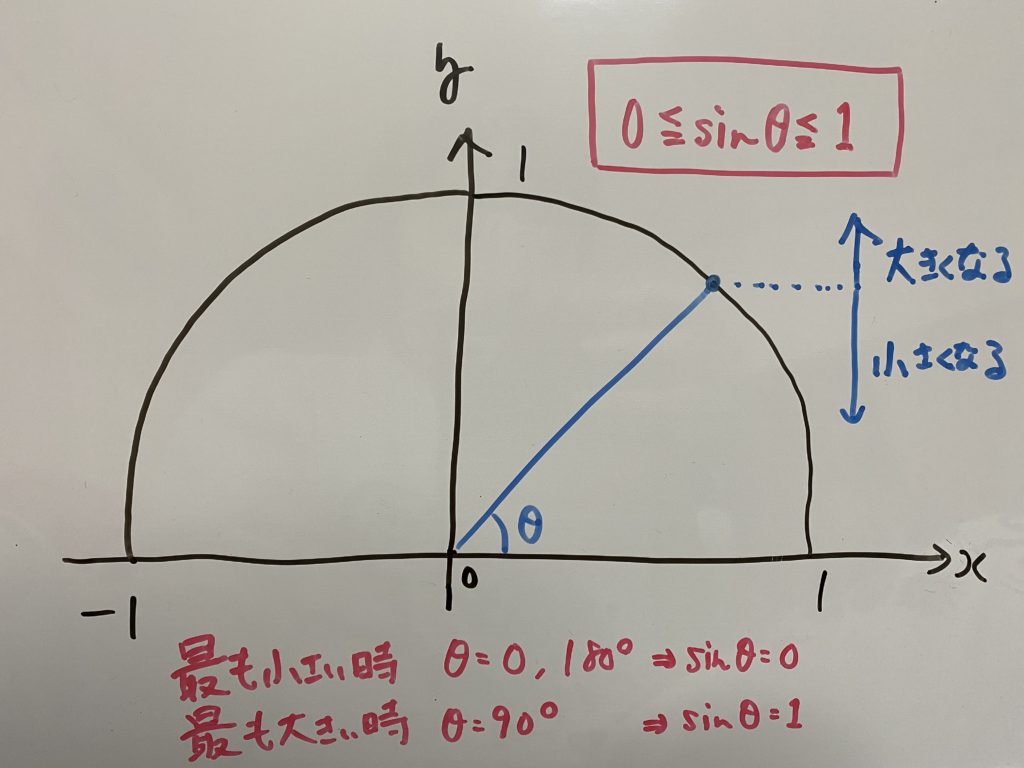
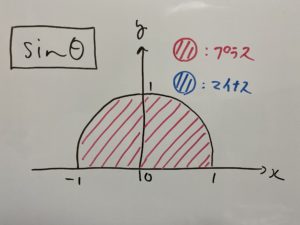
$\cos θ$は$θ$によってどう変わるか?
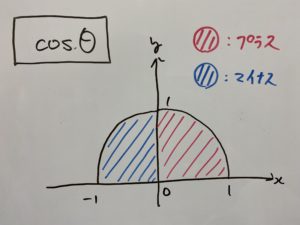
$\tan θ$は$θ$によってどう変わるか?
こちらは$0° \leqq θ\lt 90°$と$90° \lt θ \leqq 180°$で分けて説明します。
$0° \leqq θ\lt 90°$の場合
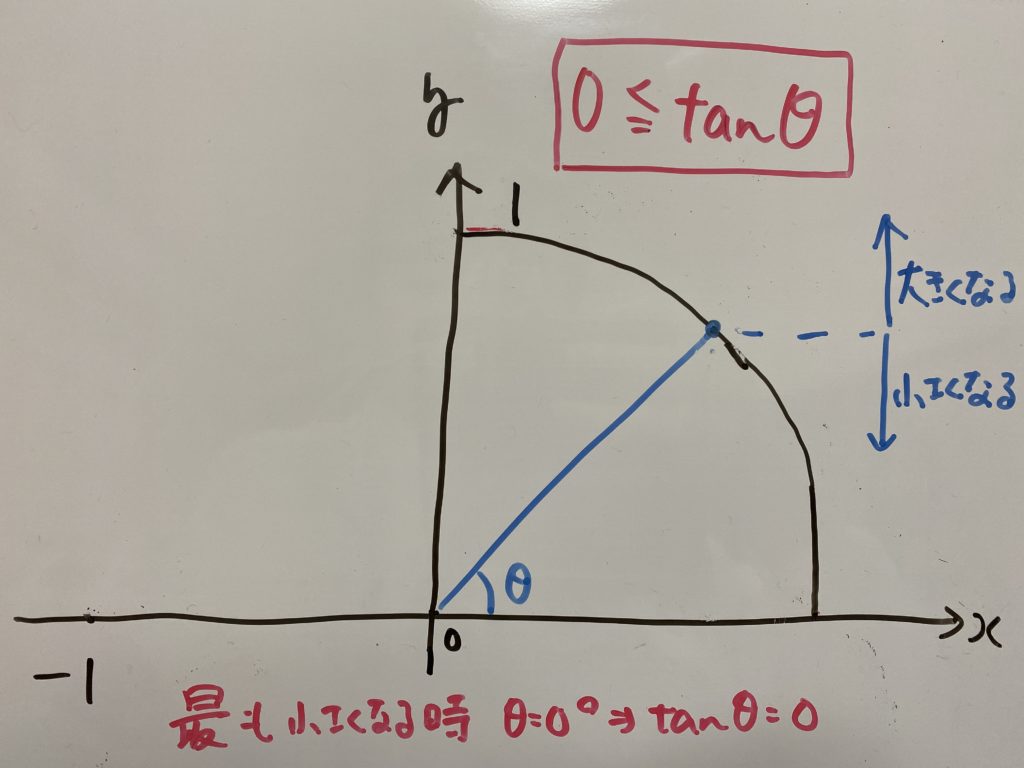
$90° \lt θ \leqq 180°$の場合
練習問題
では上の公式を用いた簡単な練習問題を解いてみましょう!
次の式の値を求めなさい。
(1)$\sin 120°$
先程の$\sin (180°-θ)=\sin θ$を用いて
$\sin 120°=\sin (180°-60°)=\sin 60°=\frac{\sqrt {3}}{2}$

$\sin 60°=\frac{\sqrt 3}{2}$は中学数学で学びましたね?
覚えていますか?忘れてしまっている方は今一度復習しましょう!
(2)$\cos 135°$
先程の$\cos (180°-θ)=-\cos θ$を用いて
$\cos 135°=\cos(180°-45°)=-\cos 45°=-\frac{1}{\sqrt {2}}$

\cos 45°=\frac{1}{\sqrt{2}}も中学数学の内容です!
$0° \leqq θ \leqq 180°$とする。次の方程式・不等式を解きなさい。
この問題を解くには『半径1の半円』を考える必要があります。

全問題この図を使って解説します!
(1)$3\cos θ +3=0$
$3\cos θ=-3$
$\cos θ=-1$
これを満たすには
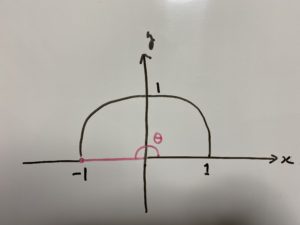
の場合ですので
$θ=180°$
(2)$3\tan θ + \sqrt{3} = 0$
$3\tan θ=-\sqrt{3}$
$\tan θ=-\frac{1}{\sqrt{3}}$
これを満たす半円上の三角形はこちらです。
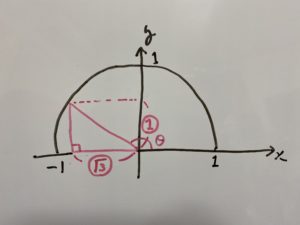
三角形を切り抜くと
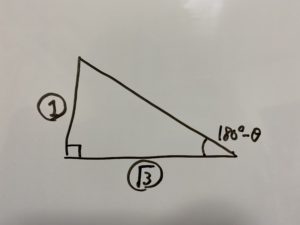
見覚え無いですか?中学で習ったこの三角形です!
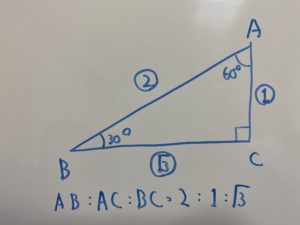
したがって
$θ=150°$
(3)$\cos θ \leqq -\frac{1}{2}$
まず半円を書いてみましょう。
$\cos θ=-\frac{1}{2}$の時次のような三角形ができますね?
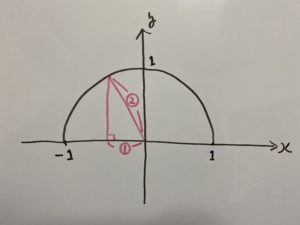
これは先程の三角形になります。
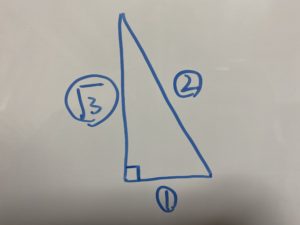
したがって$\cos θ=-\frac{1}{2}$の時$θ=120°$
今回は$\leqq \frac{1}{2}$ですので
$120° \leqq θ \leqq 180°$
(4)$\sqrt{3}\tan θ-1 \leqq 0$
まずは式変形します。
$\sqrt{3}\tan θ \leqq 1$
$\tan θ \leqq \frac{1}{\sqrt{3}}$
さて半円を書いてみましょう。
直角を挟んで両辺の比率が$1:\sqrt{3}$なので
のような三角形ということになります。
つまりこの時$θ=30°$です。
またここから左に行くほど$\tan θ$は小さくなるので、$0 \leqq θ \leqq 30°$
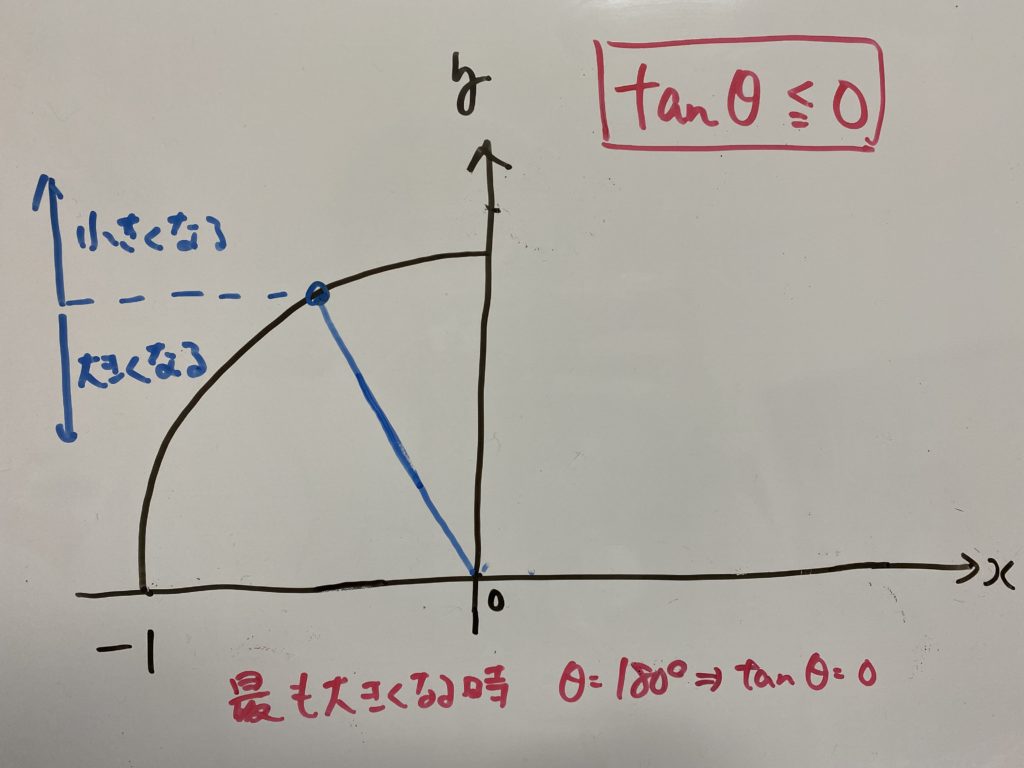
で終わりではありませんからね!!!!!
をみてみましょう。
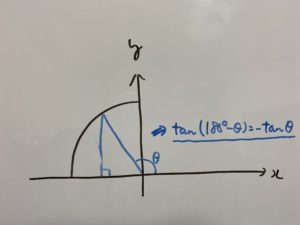
この部分は$\tan (180°-θ)=-\tan θ$のため必ずマイナスになります。
したがって$90° \leqq θ \leqq 180°$では常に$\tan θ \leqq \frac{1}{\sqrt{3}}$を満たしているわけです。
ということで正解は $0 \leqq θ \leqq 30°$、$90° \leqq θ \leqq 180°$
最後に
三角比はこの辺りから難しくなってくる気がします。つまりつまづく人が増えてくるということですね!

やるしかねぇ…。
できるだけ分かりやすい解説記事を心がけていきますのでがんばりましょう!!!



