【高校数A】『組み合わせ』の基礎を元数学科が解説する！【苦手克服】

ジル

みなさんおはこんばんにちは。

最近暑さで体調悪くしているジルでございます！

前回の記事では『順列』について解説しました。

次は『組み合わせ』の解説です。

組み合わせの定義
重複組み合わせ

この辺りを解説しようと思いますので最後までご覧くださいね！

組み合わせの定義
重複組み合わせ
1. 練習問題④
まとめ

組み合わせの定義

異なるn個のものから異なるr個を選ぶことを組み合わせといいます。

組み合わせの個数を $_{n} C_{r}$ で表します。

_{n} C_{r}

=異なるn個のものから異なるr個を選ぶ組み合わせの総数

例えば「A,B,C,D,Eから３文字選ぶ」組み合わせの総数は

_{5} C_{3}

と表せる訳です！

ジル

『順列』は並べますが、『組み合わせ』は並べません。

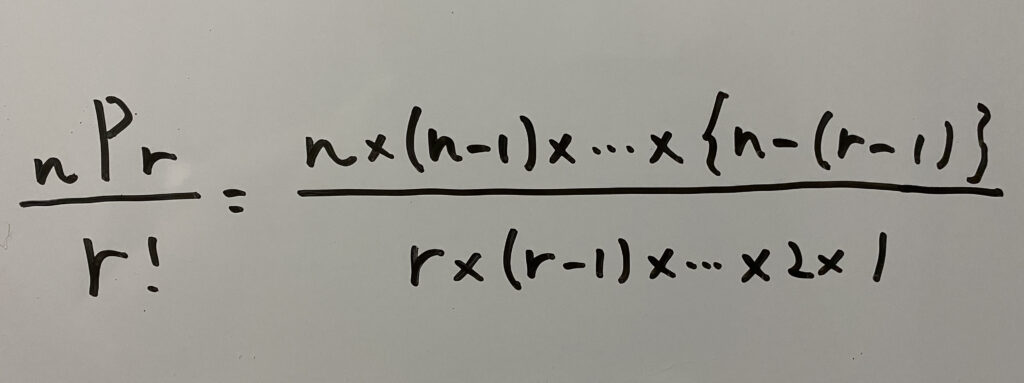
順列の場合は『A-B-C』と『B-A-C』は違いますが組み合わせの場合は『A-B-C』と『B-A-C』は同じです。

次に

_{n} C_{r}

の計算方法ですが

_{n} C_{r} = \frac{_{n} P_{r}}{r!}

もう少し計算すると

例えば先ほどの

_{5} C_{3}

は

_{5} C_{3} = \frac{_{5} P_{3}}{3!} = \frac{5 \times 4 \times 3}{3 \times 2 \times 1} = 10

苦戦しつつ調べるあざらし

今更ですが $_{n} P_{r}$ ってなんや…？？

ジル

そんな貴方のために順列に関する記事を下に貼っておきますのでご覧ください！

【高校数A】『順列』の基礎を元数学科が解説する！【苦手克服】

今回は【高校数学】【数A】『場合の数と確率』から順列について、基礎を徹底解説しました。順列の定義から円順列、じゅず順列などまで網羅しました。苦手な方でもわかりやすくしたつもりですのでぜひご覧ください。

ここで１つ

_{n} C_{r}

の性質。

_{n} C_{r} =_{n} C_{n}_{-}_{r}

先ほど計算した

_{5} C_{3}

は

_{5} C_{3} =_{5} C_{5}_{-}_{3} =_{5} C_{2}

と式変形できます。

ジル

$_{n} C_{r}$ のrの部分が小さいほど計算簡単ですのでその辺意識して、必要に応じて式変形するといいと思います！

また

_{n} C_{n} =_{n} C_{0} = 1

も覚えておくように！

では

_{n} C_{r}

を求める練習問題を解いてみましょう。

練習問題①

（１） $_{6} C_{2}$

（２） $_{4} C_{3}$

（３） $_{3} C_{0}$

（４） $_{9} C_{7}$

（５） $_{5} C_{5}$

まあ組み合わせの問題で一番基礎的なやつです。

必要に応じて

$_{n} C_{r} =_{n} C_{n}_{-}_{r}$

を使うことを意識しましょう！

（１）の解答

$_{6} C_{2} = \frac{_{6} P_{2}}{2!} = \frac{6 \times 5}{2 \times 1} = 15$

（２）の解答

ジル

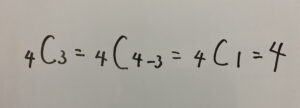
こちらはの計算式、何故か上手く表示できませんでしたので画像を載せておきます。

（３）の解答

$_{3} C_{0} = 1$

（４）の解答

$_{9} C_{7} =_{9} C_{2} = \frac{9 \times 8}{2 \times 1} = 36$

（５）の解答

$_{5} C_{5} = 1$

練習問題②

７人の生徒から文化委員を３人決めます。

その組み合わせの数を求めなさい。

$_{7} C_{3} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35$

答えは35通り。

練習問題③

男性４名、女性３名から３名の代表者を選出します。

この時、次の条件を満たして選出する場合の組み合わせの総数を求めなさい。

（１）男性１名、女性２名

（２）特定の２名がいる

（３）少なくとも１名は女性

（１）の解答

「４名の男性から１名を選ぶ」かつ「３名の女性から２名を選ぶ」ことから

「４名の男性から１名を選ぶ」は

$_{4} C_{1} = 4$

「３名の女性から２名を選ぶ」は

$_{3} C_{2} = 3$

積の法則より、 $4 \times 3 = 12$

答えは12通り。

（２）の解答

「特定の２名」を選ぶ候補から外します。すると残り５名から１名を選ぶことになるので

$_{5} C_{1} = 5$

答えは５通り。

（３）の解答

この時は「女性が１名の場合」と「女性が２名の場合」と「女性が３名の場合」で場合分けをして和の法則より足せば解けます。

「女性が１名の場合」

男性２名と女性１名を選べば良いので

$_{4} C_{2} \times_{3} C_{1} = 6 \times 3 = 18$

「女性が２名の場合」

男性１名と女性２名を選べば良いので

$_{4} C_{1} \times_{3} C_{2} = 4 \times 3 = 12$

「女性が３名の場合」

１通り。

したがって

$18 + 12 + 1 = 31$

答えは３１通り。

重複組み合わせ

異なるn個からr個、同じものを繰り返しとっても良いものとして選ぶ組み合わせの総数は

_{n}_{+}_{r}_{-}_{1} C_{r}

こちら有名な証明方法があるので紹介します。

例として

「a,b,c,d,eから３文字、同じものをとっても良いものとして３文字選ぶ組み合わせの総数はいくつでしょうか？」

の問題を使って証明してみます。

まず３個の”○”と５-1個の”|”を用意します。

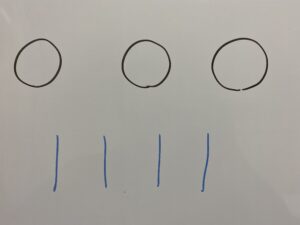
次の順序で考えます。

①”|”を4つ書きます。

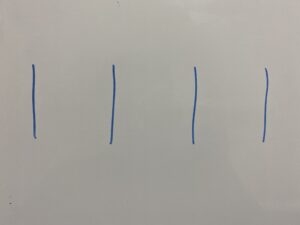
②”○”3つを”|”の間、または左端・右端に入れます。

この時”|”の間、左端、右端に次のような意味を与えます。

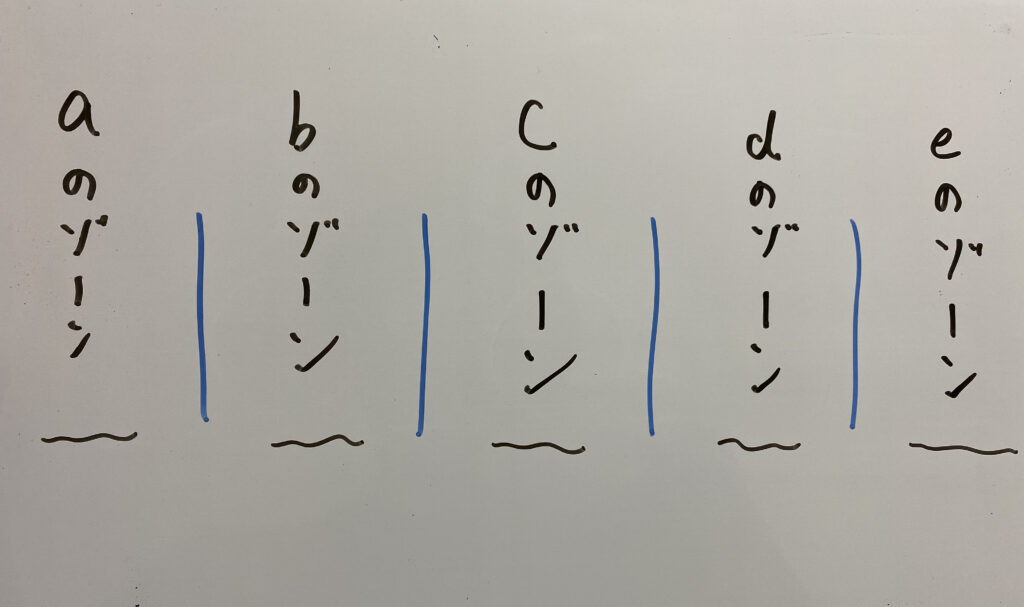
つまりこういうことです。

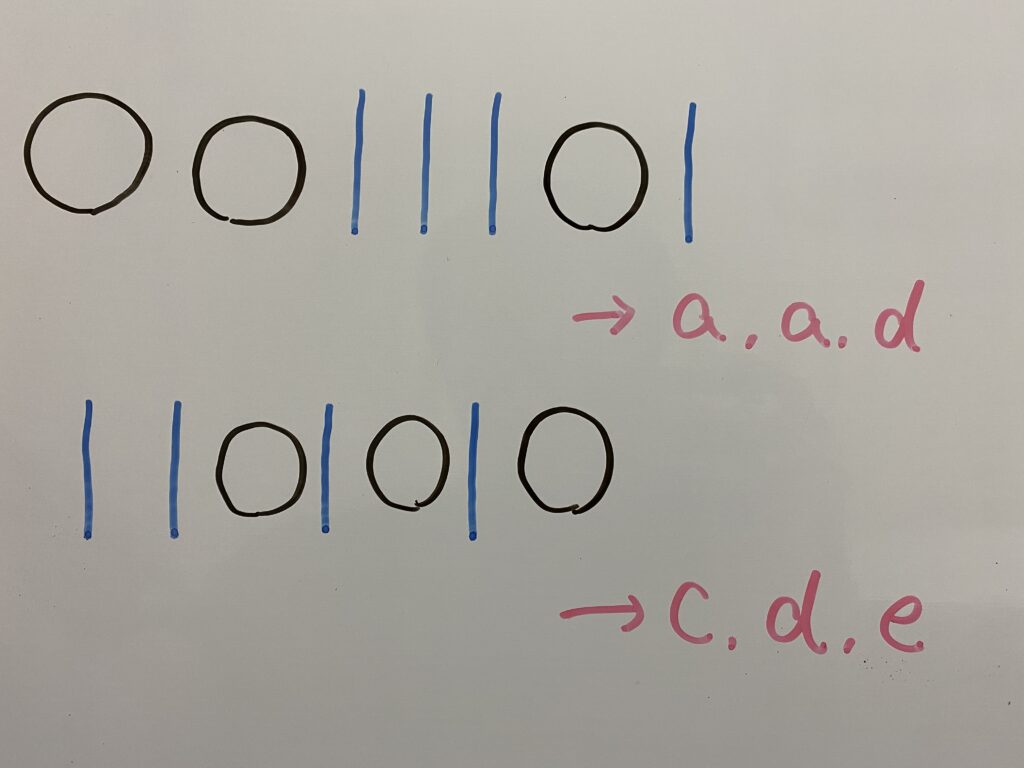
この全パターンを数えれば求められます。

ジル

さて、察しの良い方はお気づきでしょうか…？

“○”３つと”|”４つの並び方の総数を求めればいいんですよこれが！

これは前回の記事で解説した「同じものを含む順列」を利用すれば解けますね？

n個のうち、同じものがa個、b個、c個、…あるものとする。
その並べ方の総数は

\frac{n!}{a! \times b! \times c! \times \dots}

（ただしa+b+c+…=n）

つまり

\frac{7!}{3! \times 4!} =_{7} C_{3} =_{3}_{+}_{(}_{5}_{-}_{1}_{)} C_{3}

練習問題を解いてみましょう！

練習問題④

ショートケーキ、チーズケーキ、モンブランがあります。

これらを使って６個入りのケーキセットを作る時、その組み合わせの総数は何通りか求めなさい。

異なる３個から６種類、同じものを繰り返し選んで良いものとした組み合わせなので

$_{3}_{+}_{6}_{-}_{1} C_{6} =_{8} C_{6} =_{8} C_{2} = \frac{8 \times 7}{2 \times 1} = 28$

答えは２８通り。

まとめ

【組み合わせの定義】

_{n} C_{r}

=異なるn個のものから異なるr個を選ぶ組み合わせの総数

【重複組合せ】
異なるn個からr個、同じものを繰り返しとっても良いものとして選ぶ組み合わせの総数は

_{n}_{+}_{r}_{-}_{1} C_{r}

順列と組み合わせの違いをしっかり理解しましょう。

テストでは両方混ざって出題されるので、これは順列に関する問題なのか組み合わせに関する問題なのか区別できるようにすると良いですね。

ジル

楽しい数学Lifeを！