
みなさんおはこんばんにちは。
最近週一でラーメン食べたくなるジルでございます!
今回は『データの分析』という分野の解説をしていきます。
基礎の確認

いくつかの単語を確認しましょう。
度数分布
度数分布とは統計において、標本として得たある変量の値のリストのことです。
高校数一において度数分布は度数分布表かヒストグラムで分かりやすく表されます。
◎度数分布表
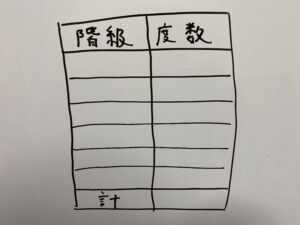
このような表です。
◎ヒストグラム
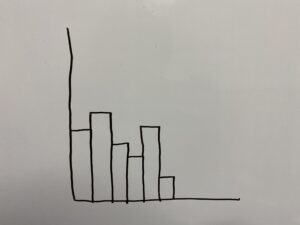
このようなグラフです。

例にした度数分布表、ヒストグラムは両方同じ度数分布を使っています。
度数…各階級に入っている数。
階級値…階級の真ん中の値。

ちなみに階級の欄には今回の例のように”○〜○”と区間で書いてあるパターンもあれば、”○”と一つの数字になっているパターンもあります。
最頻値…最も頻出している値。
中央値…データを大きさ順に並べた時、そのなかで真ん中の値。

3つ合わせて『代表値』と言います。
練習問題をやってみよう

基礎内容を頭に叩き込むために、練習問題をいくつか解いてみましょう。
問1(度数分布表①)
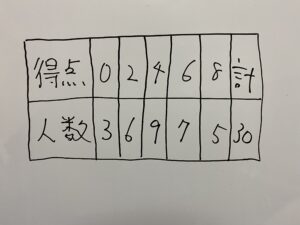
上の表は30人がゲームをした時の得点をまとめた度数分布表です。
この時、得点の平均値、中央値、最頻値を求めなさい。
《解答》
平均値
分かっているデータの個数:30
それぞれの得点:0点が3人、2点が6人、4点が9人、6点が7人、8点が5人
したがって
$\dfrac{1}{30}(0 \times 3 + 2 \times 6 + 4 \times 9 + 6 \times 7 + 8 \times 5)=\frac{12+36+42+40}{30}=\frac{132}{30}=4.4$
中央値
データを小さい順に並べてみましょう。
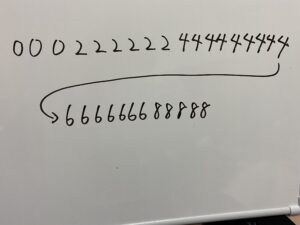
その中で真ん中は
ですね?

いやいや、そこ何も数字ありませんけど笑

データの個数が偶数の場合はそうなるんですよね。そんな時はその位置の両側にある値の平均値が中央値になります。
したがって中央値は
$\frac{1}{2}(4+4)=4$
最頻値
こちらは度数分布表を見れば一目瞭然。4点が一番多いです。
問2(度数分布表②)
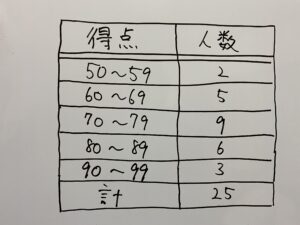
25人の生徒が数学のテストを受け、データ化して度数分布表にしたものです。
この時
(1)得点の平均値として考えられるものの中で、最大のものを求めなさい。
(2)得点の平均値として考えられるものの中で、最小のものを求めなさい。
⇩
各階級の値の中で最大の数で平均値をとったもの”平均値として考えられるもので最小のもの”
⇩
各階級の値の中で最小の数で平均値をとったもの
《解答》
(1)
まず度数分布表を見てみましょう。
各階級値の中で最大の数はそれぞれ59、69、79、89、99であるため
2人が59点、5人が69点、9人が79点、6人が89点、3人が99点だった場合の平均値を求めれば良いですね?
$\dfrac{1}{25}(59 \times 2 + 69 \times 5 + 79 \times 9 + 89 \times 6 + 99 \times 3)$
$=\dfrac{1}{25}(118+345+711+534+297)=\frac{2005}{25}=80.2$
(2)
まず度数分布表を見てみましょう。
各階級値の中で最小の数はそれぞれ50、60、70、80、90であるため
2人が50点、5人が60点、9人が70点、6人が80点、4人が90点だった場合の平均値を求めれば良いですね?
$\dfrac{1}{25}(50 \times 2 + 60 \times 5 + 70 \times 9 + 80 \times 6 + 90 \times 3)$
$=\dfrac{1}{25}(100+300+630+480+270)=\frac{1780}{25}=71.2$
問3(ヒストグラム)
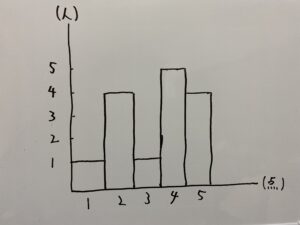
上の図は15人がサッカーのPKを5回行い、その得点データをヒストグラムにしたものである。この時
(1)最頻値を求めなさい。
(2)中央値を求めなさい。
(3)平均値を求めなさい。
《解答》
(1)
ヒストグラムを見てみましょう。一番頻出した得点は4点です。したがって最頻値は4点。
(2)
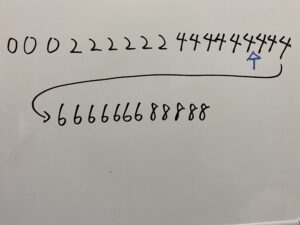
小さい順で全て並べると
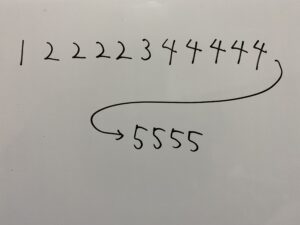
真ん中は
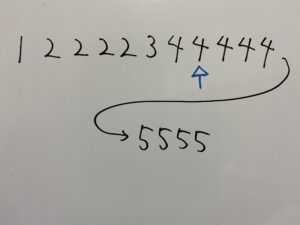
したがって中央値は4点。
(3)
$\dfrac{1}{15}(1+2 \times 4 + 3 \times 1 +4 \times 5 +5 \times 4)=\frac{51}{15}=3.4$
最後に

今回の分野、実は私が高校生の頃は数Iの必修科目にありませんでした。
調べてみるとどうやら2012年度から導入されたみたいですね。

私も改めて勉強しました。
いやはや、人類一生勉強ですね。また一つ賢くなりました(^∇^)

楽しい数学Lifeを!



