【高校数I】二次方程式の判別式を元数学科が解説【苦手克服】

前回の記事では二次方程式の基本のキを勉強しました。

次に学ぶべきなのは『判別式』でございます。

今回この判別式に焦点を当てていきます。

そもそも『判別式』とは？？

すなわち

二次方程式において、実数解が何個存在するかを調べるための式

です。こちらそんなに難しくないので頑張って理解してみてください！

 

$ax^2+bx+c=0$において

$D=b^2-4ac$とします。

この時の$D$が正の数か負の数か、はたまた０かによって判別します。

$D \gt 0$の場合

実数解は２つです。

$D=0$の場合

実数解は１つです。

１つだけの解を『重解』といいます。

$D \lt 0$の場合

実数解は存在しません。

判別式を使った練習問題を解いてみよう！

一通り判別式の説明を終えたところで、練習問題を解いてみましょう！

 

$２x^2-5x+2=0$の実数解の数を求めよ。

まずはこちらを解いていきます。

$D=b^2-4ac$に当てはめてみましょう。$a=2$、$b=-5$、$c=2$ですね？

よって

$D=(-5)^2-4 \times 2 \times 2=25-16=9 \gt 0$

したがって実数解は2つ。

 

$x^2-x+5=0$の実数解の数を求めよ。

先ほどと同じカンジで解いていきます。

$a=1$、$b=-1$、$c=5$です。

$D=(-1)^2-4 \times 1 \times 5=1-20=-19 \lt 0$

したがって実数解は存在しない。

 

 

$x^2+6x+9=0$の実数解の数を求めよ。

$a=1$、$b=6$、$c=9$です。

$D=6^2-4 \times 1 \times 9=36-36=0$

したがって実数解は１つ。

そもそもなんで$D=b^2-4ac$で解の数が分かるの？

さて今まで$D=b^2-4ac$の判別式を当たり前に使ってきました。

正直これは覚えて貰えば十分ですが、なぜこうなるのか？と疑問に持ったアナタのために説明しました！

 

$D=b^2-4ac$で実数解の数が分かる理由

まずは中学数学を振り返りましょう。『連立方程式』についてです。

\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 8 \\
2x + 4y = 4
\end{array}
\right.
\end{eqnarray}

こんな形のやつです。

ちなみにこの連立方程式の解は$x=14$、$y=-6$です。

みなさんこの解がどういう意味を持つか知っていますか？

先ほどの連立方程式の2つの式を少し変形してみましょう。

$x+y=8 \Rightarrow y=-x+8$

$2x+4y=4 \Rightarrow x+2y=2 \Rightarrow 2y=-x+2 \Rightarrow y=-\frac{1}{2}+1$

このように一次関数の式になります。先ほどの$x=14$、$y=-6$は

二つの関数の交点になります。

つまり、$y=-x+8$と$y=-\frac{1}{2}+1$との交点は$(14,-6)$ということです。

 

この関係は覚えておきましょう。色々応用ができます。

 

さてここから本題です。

$ax^2+bx+c=0$について

\begin{eqnarray}
\left\{
\begin{array}{l}
y = ax^2 +bx +c \\
y = 0
\end{array}
\right.
\end{eqnarray}

という連立方程式を解く手順で、$y$同士でつなげてできた方程式の形ですよね？これ分かりますか？

ここで先ほどの

 

$連立した２つの方程式の解　\Leftrightarrow　二つの方程式の交点$

の考え方を使います。

この関係性が成り立つわけです。

 

したがって、$y=ax^2+bx+c$と$y=0$の交点の数が$ax^2+bx+c=0$の解の数になるんですね！

$y=0$というのは$x$軸のことですね。

ここで$y=ax^2+bx+c$を平方完成してみましょう。（ここでは$a=0$とします。）

 

$y=a(x^2+\frac{b}{a}x)+c=a\{(x^2+\frac{b}{2a}x+\frac{b^2}{4a^2})-\frac{b^2}{4a^2}\}+c$

$=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}+c=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}$

これで平方完成できました。

さあこの式と$x$軸との交点の数の場合わけは、aがプラスかマイナスかで変わってきます。

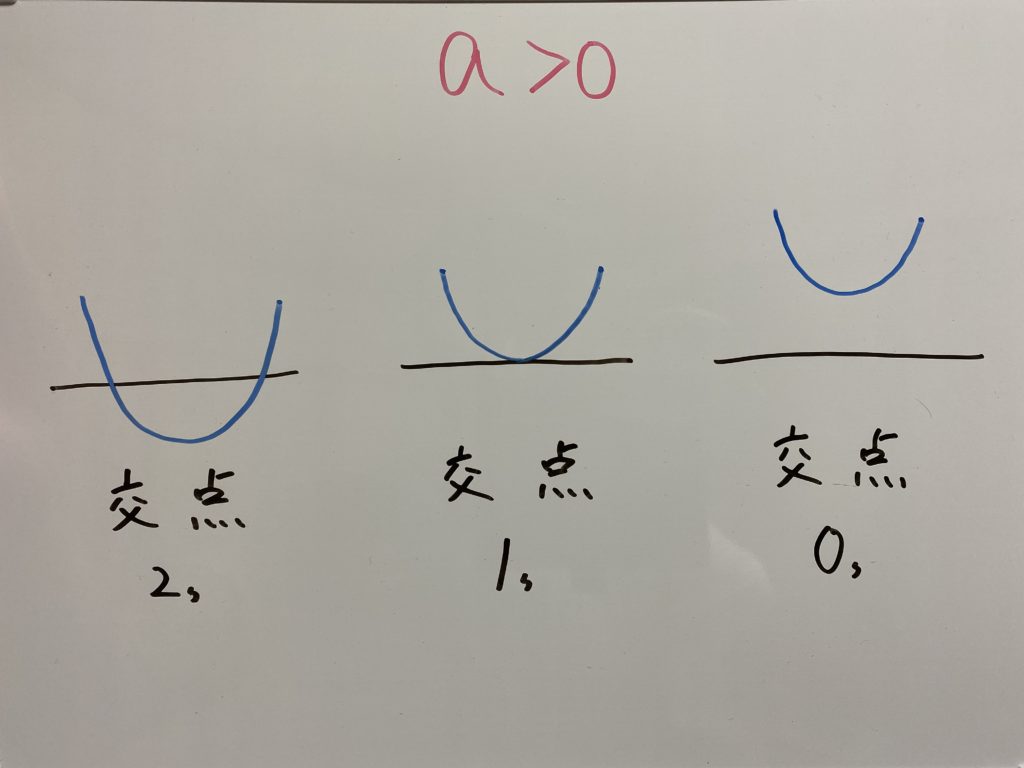
この場合わけで重要なのは『頂点の$y$座標がプラスかマイナスか』です。

頂点に注目してみましょう。$(-\frac{b}{2a},-\frac{b^2-4ac}{4a})$です。

 

❶$a \gt 0$の場合

頂点の$y$座標$-\frac{b^2-4ac}{4a}$について

分母の$4a$は$a \gt 0$なので$4a \gt 0$なのは明らかです。

よって$-\frac{b^2-4ac}{4a}$は

$b^2-4ac \gt 0 \Rightarrow -\frac{b^2-4ac}{4a} \lt 0$

$b^2-4ac = 0 \Rightarrow -\frac{b^2-4ac}{4a} = 0$

$b^2-4ac \lt 0 \Rightarrow -\frac{b^2-4ac}{4a} \gt 0$

になります。

 

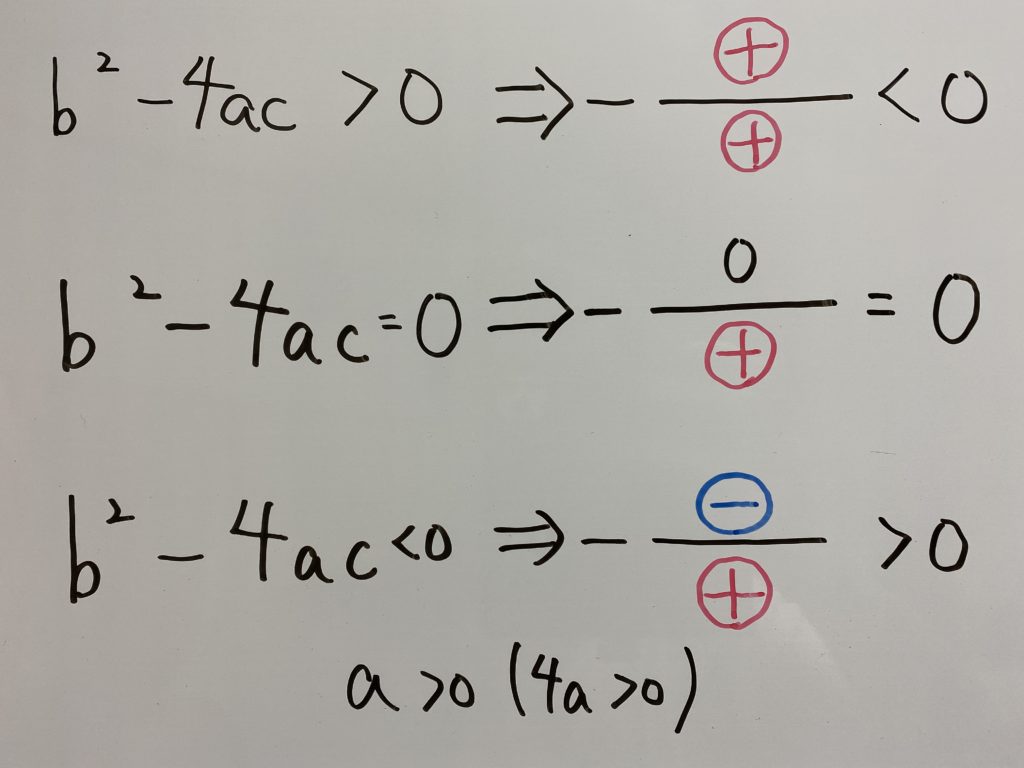
先ほどの画像をもう一度見てみましょう。

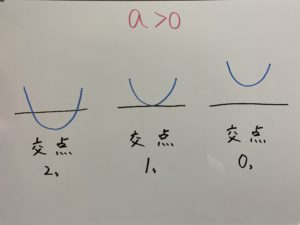
頂点の$y$座標がマイナスの時は交点2つ、0の時は交点1つ、プラスの時は交点0つですね？

したがって、$a \gt 0$の時

$D \gt 0 \Rightarrow 頂点のy座標はマイナス \Rightarrow 交点2つ$

$D = 0 \Rightarrow 頂点のy座標は0 \Rightarrow 交点1つ$

$D \lt 0 \Rightarrow 頂点のy座標はプラス \Rightarrow 交点0つ$

 

❷$a \lt 0$の場合

頂点の$y$座標$-\frac{b^2-4ac}{4a}$について

分母の$4a$は$a \lt 0$なので$4a \lt 0$なのは明らかです。

よって$-\frac{b^2-4ac}{4a}$は

$b^2-4ac \gt 0 \Rightarrow -\frac{b^2-4ac}{4a} \gt 0$

$b^2-4ac = 0 \Rightarrow -\frac{b^2-4ac}{4a} = 0$

$b^2-4ac \lt 0 \Rightarrow -\frac{b^2-4ac}{4a} \lt 0$

になります。

 

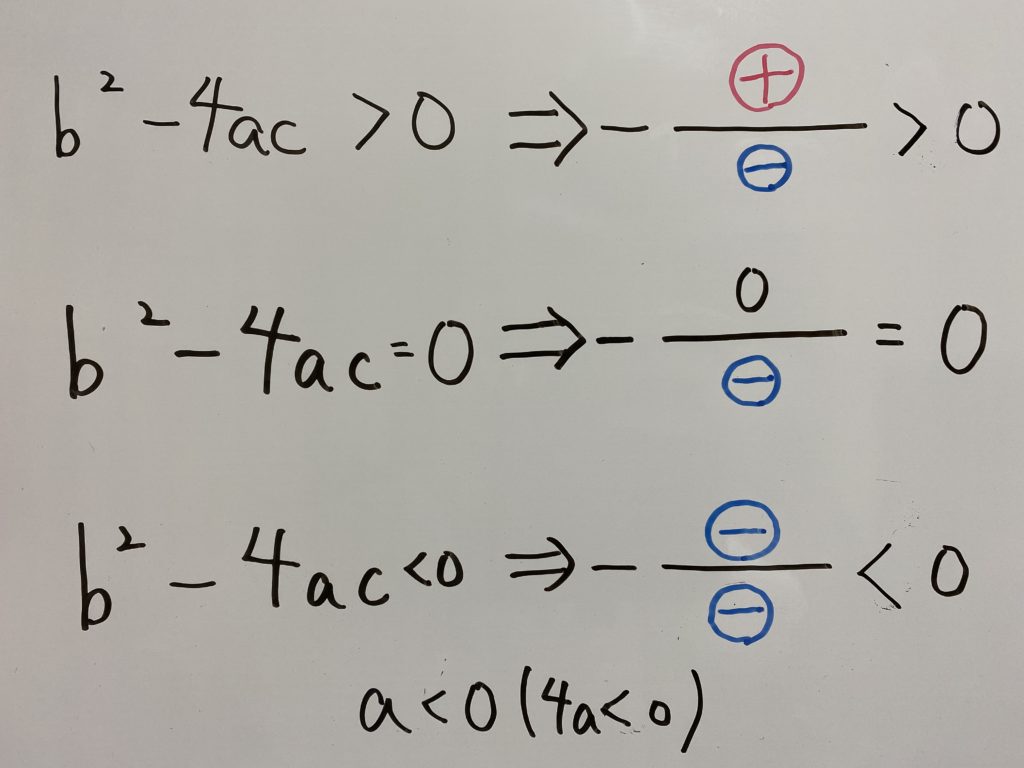
先ほどの画像をもう一度見てみましょう。

 

頂点の$y$座標がプラスの時は交点2つ、0の時は交点1つ、マイナスの時は交点0つですね？

したがって、$a \lt 0$の時

$D \gt 0 \Rightarrow 頂点のy座標はプラス \Rightarrow 交点2つ$

$D = 0 \Rightarrow 頂点のy座標は0 \Rightarrow 交点1つ$

$D \lt 0 \Rightarrow 頂点のy座標はマイナス \Rightarrow 交点0つ$

 

以上から

$b^2-4ac \gt 0 \Rightarrow 交点は2つ \Rightarrow 二次方程式の実数解は2つ$

$b^2-4ac = 0 \Rightarrow 交点は1つ \Rightarrow 二次方程式の実数解は1つ$

$b^2-4ac \lt 0 \Rightarrow 交点はなし \Rightarrow 二次方程式の実数解はなし$

最後に

今回は判別式のお話でした。

判別式の証明が思ったより長くなってしまいました笑

次は二次方程式の応用問題を解説したいなと考えております。