
みなさんおはこんばんにちは。
お酒飲みすぎて最近太ってきたジルでございます!
前回は『集合の要素の個数』の基礎中の基礎を解説しました。
最後に簡単な練習問題を解いてみましたが、今回は少しだけ前より難しいのをやってみましょう!
テーマは『要素が数えられないくらい多いパターンの問題』です。
問題
200以上500以下の自然数のうち、次の条件を満たす数は何個あるか答えなさい。
(1)6の倍数
(2)9の倍数
(3)6の倍数または9の倍数
(4)6の倍数でも9の倍数でもない数
(5)6の倍数ではあってかつ9の倍数でない数
解説に進む前に必要な知識や考え方を書き記します。
「とっとと解説みたい!」方はこちらからどうぞ!
考え方・アドバイス・知識
その①:ベン図を書こう!
面倒かもですがベン図は必ず書きましょう。
ほんとに簡単な問題ならベン図なしでも問題ないですが、基本的にはベン図は書いた方がいいです。

ベン図を書く癖をつけた方がいいですね!
その②:「以上」「以下」「から」「まで」「未満」「より大きい」「より小さい」の使い分け
数学の問題において例えば5について「5以上」「5以下」「5から」「5まで」「5未満」「5より大きい」「5より小さい」と言われた時、5は含まれるかどうか分かっていますか?
今までなんとなくやり過ごしていませんでしたか?ここらで一度しっかり確認しましょう!
5を含まない…「未満」「より大きい」「より小さい」
問題によっては重要になるので理解しておいてください。
その③:『ある範囲内の〇〇の倍数の数』の求め方
具体例を出して考えてみます。
『100から200までの3の倍数の数』を求めてみましょう。
手順その1…100を3で割る(100までの3の倍数を求める)
$100 \div 3 =33 …1$
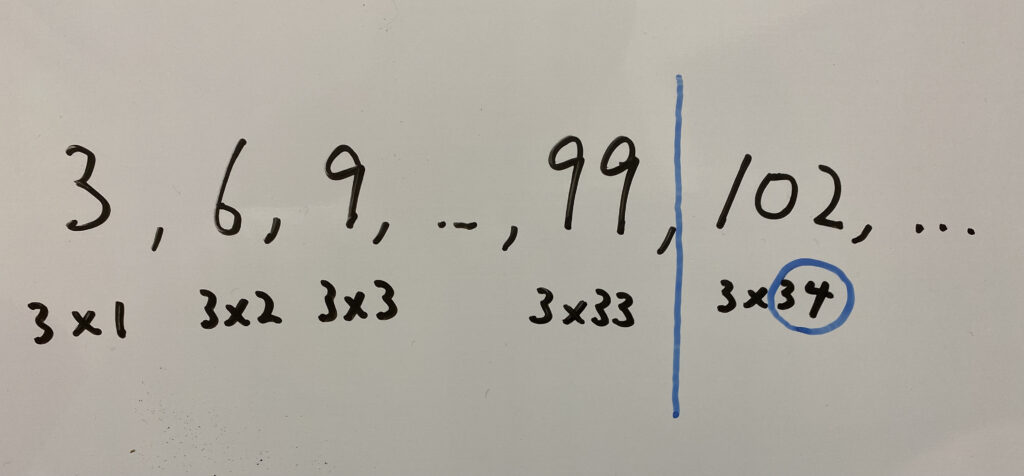
つまり、出た商+1から範囲に入ります。
手順その2…200を3で割る(200までの3の倍数を求める)
$200 \div 3 =66…2$
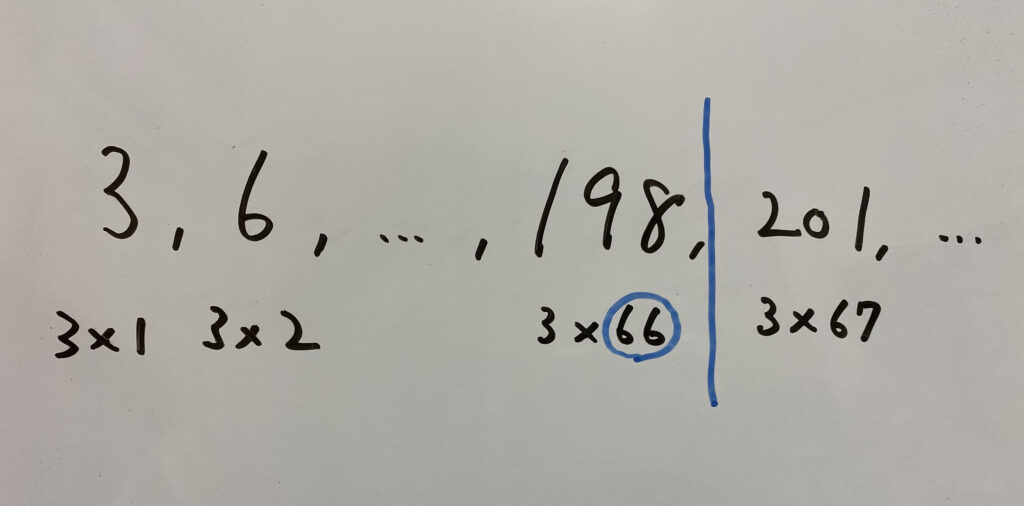
つまり出た商までが範囲に入ります。
まとめると
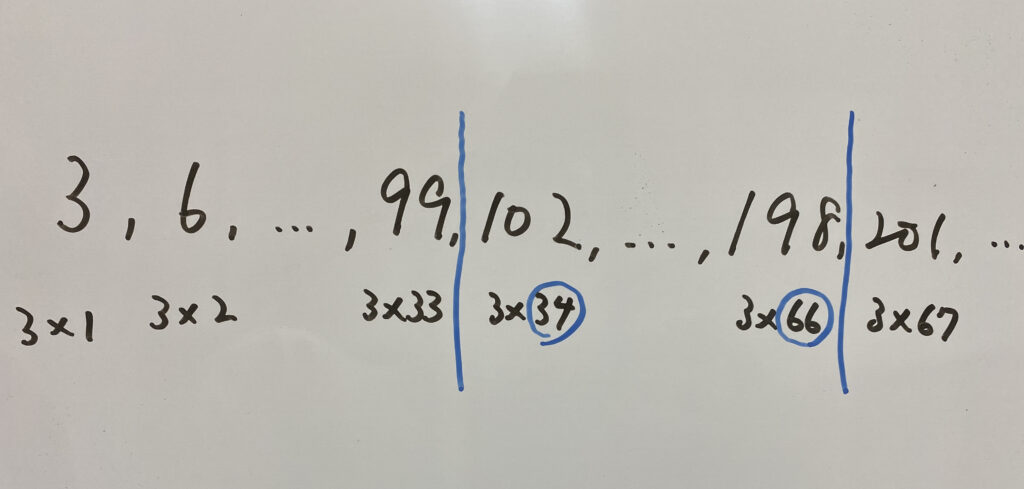
つまり3の倍数で100から200の範囲に入っているのは34番目の102〜66番目の198になります。
手順その3…数を数える

さて数えよう。
102,105,108,…

大変そうやなぁ。
計算方法教えましょう!
先程まとめた画像を使って計算すればOKです!計算方法は
(右端の丸)ー(左端の丸)+1
つまり
$66-34+1=33$
解答
前説がずいぶん長くなってしまいましたが、解答いきます。
(1)6の倍数
先程述べた「その③:『ある範囲内の〇〇の倍数の数』の求め方」の考え方を利用すれば楽勝です。
$200 \div 6=33…2$
$500 \div 6=83…2$
つまり
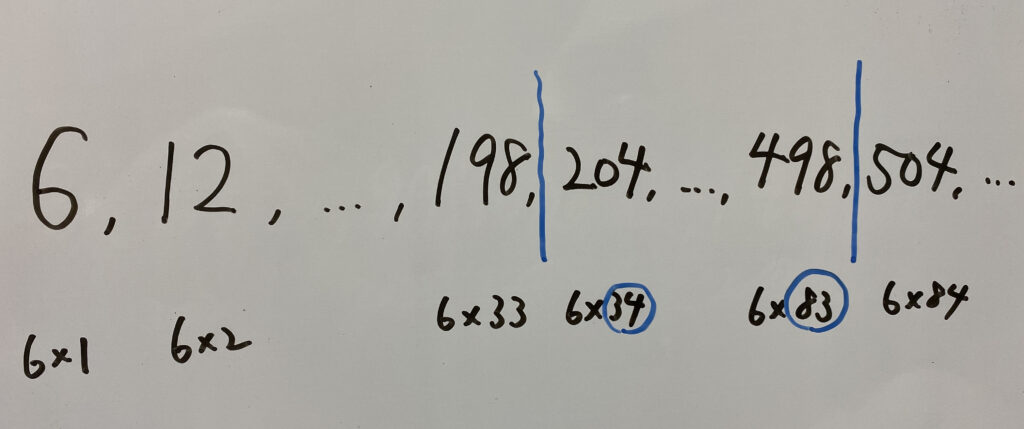
したがって
$83 – 34 +1= 50$
答えは50
(2)9の倍数
これも(1)と同じく「その③:『ある範囲内の〇〇の倍数の数』の求め方」を利用しましょう!
$200 \div 9=22…2$
$500 \div 9=55…5$
したがって
$55-23+1=33$
答えは33
(3)6の倍数または9の倍数
分かりやすく解説するために次を定義します。
$U={200以上500以下の自然数の集合}$
$A={6の倍数の集合} \subset U$
$B={9の倍数の集合} \subset U$
今回求めたい個数が「200以上500以下で、6の倍数または9の倍数」なのでつまり
$n(A \cup B)$ですね。
ここで確認したいのが
和集合の要素の個数の求め方です。
ある集合A,Bについてその和集合の要素の個数は
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

わ、わからん…:(;゙゚’ω゚’):
答えは、6と9の最小公倍数である18です。

みなさん、最小公倍数・最大公約数は覚えていますか?
念のために確認しておきましょうかね(^∇^)
最小公倍数(さいしょうこうばいすう、英: least common multiple)とは、ではない複数の整数の公倍数のうち最小の自然数をさす。たびたび、L.C.M.やlcm等の省略形で記述される。
「キリスト教」『フリー百科事典 ウィキペディア日本語版』。2021年4月14日 (水) 03:23 UTC、URL: https://ja.wikipedia.org
最大公約数(さいだいこうやくすう、英: greatest common divisor)とは、少なくとも一つが0ではない複数の整数の公約数のうち最大の数を指す。具体的にはユークリッドの互除法により求めることができる。
「キリスト教」『フリー百科事典 ウィキペディア日本語版』。2021年4月14日 (水) 03:09 UTC、URL: https://ja.wikipedia.org
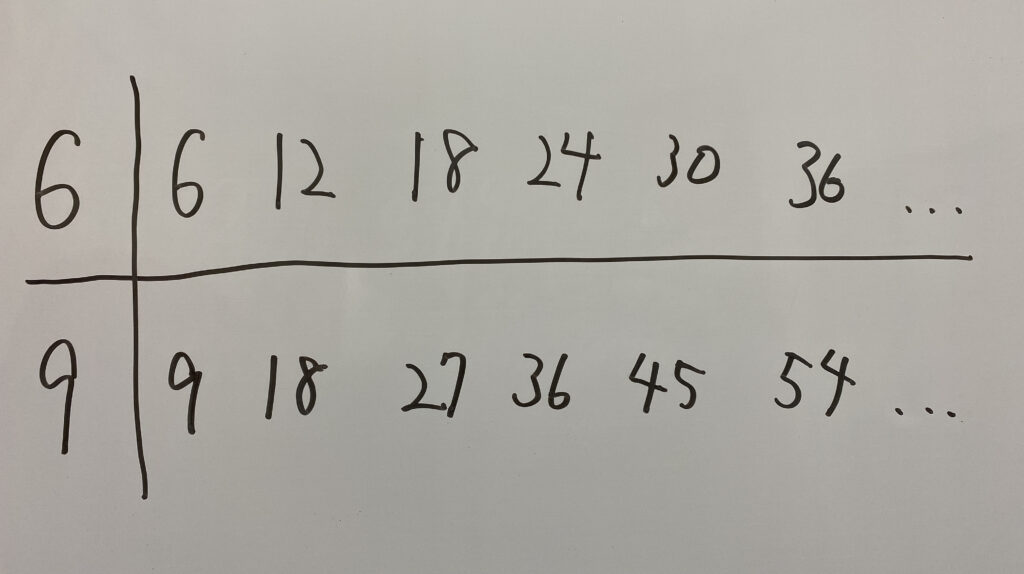
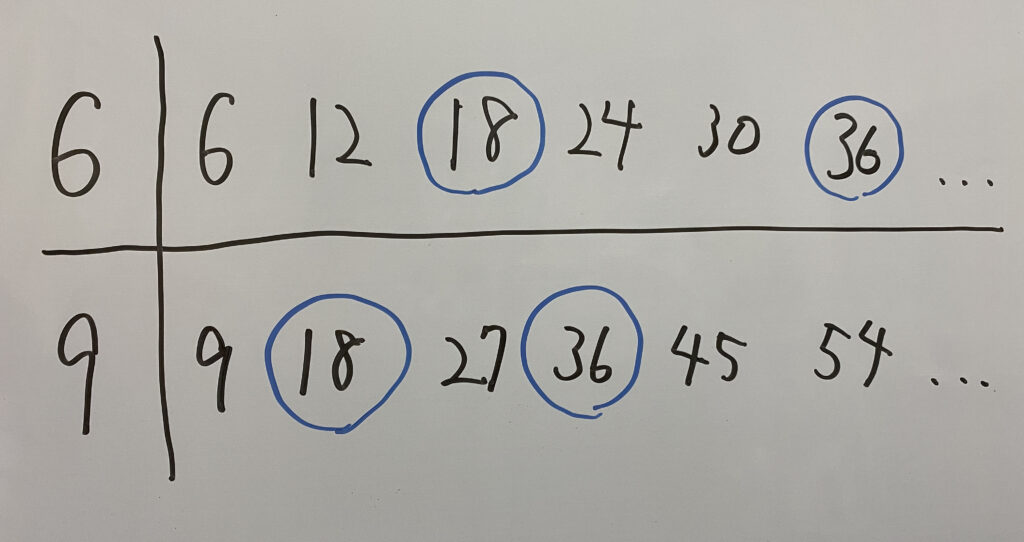
「その③:『ある範囲内の〇〇の倍数の数』の求め方」を利用しましょう!
$200 \div 18=11…2$
$500 \div 18=27…14$
したがって
$27-12+1=16$
したがって$n(A \cap B)=16$
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$であるため
$n(A)=50$、$n(B)=33$、$n(A \cap B)=16$を代入して
$n(A \cup B)=50+33-16=67$
答えは67
(4)6の倍数でも9の倍数でもない数

まずは今まで求めてきた個数を利用できないか考えます。
まずはベン図を書きましょう。今回求めたい部分は斜線のところ
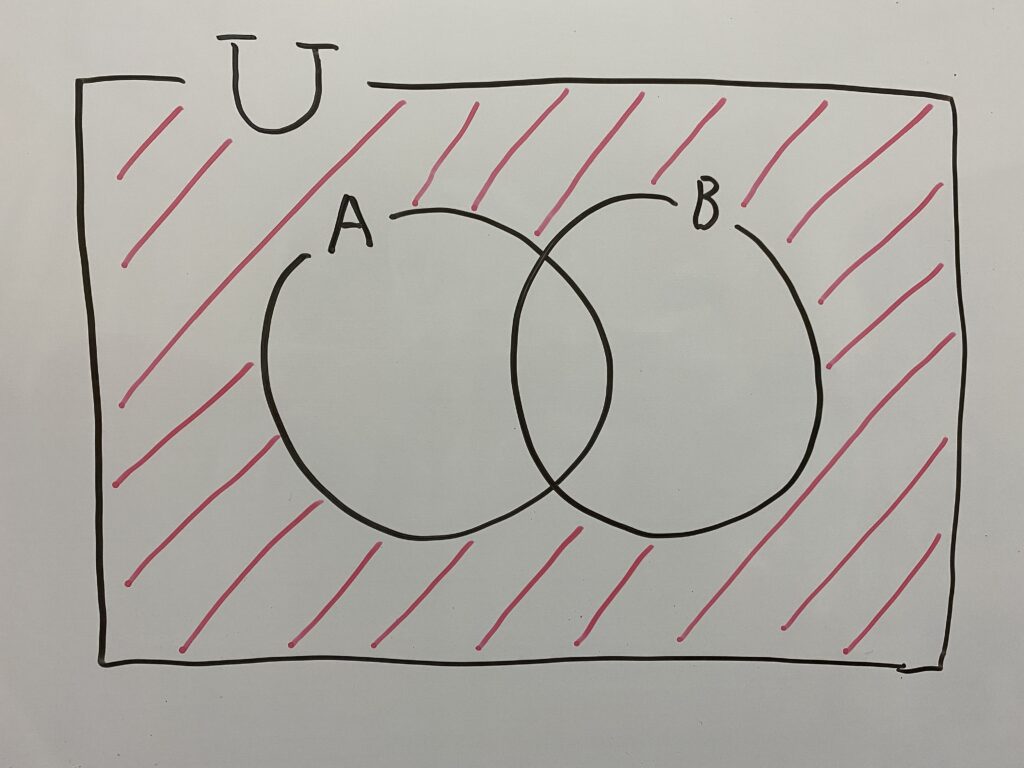

ベン図書くと分かりやすい!
一目でわかりますね?
$n(U)-n(A \cup B)$
$n(A \cup B)=16$は(3)で求めましたので、
$n(U)-n(A \cup B)=301-67=234$
答えは234
(5)6の倍数ではあってかつ9の倍数でない数
こちらも文字だけではわかりづらいためベン図を書きましょう。
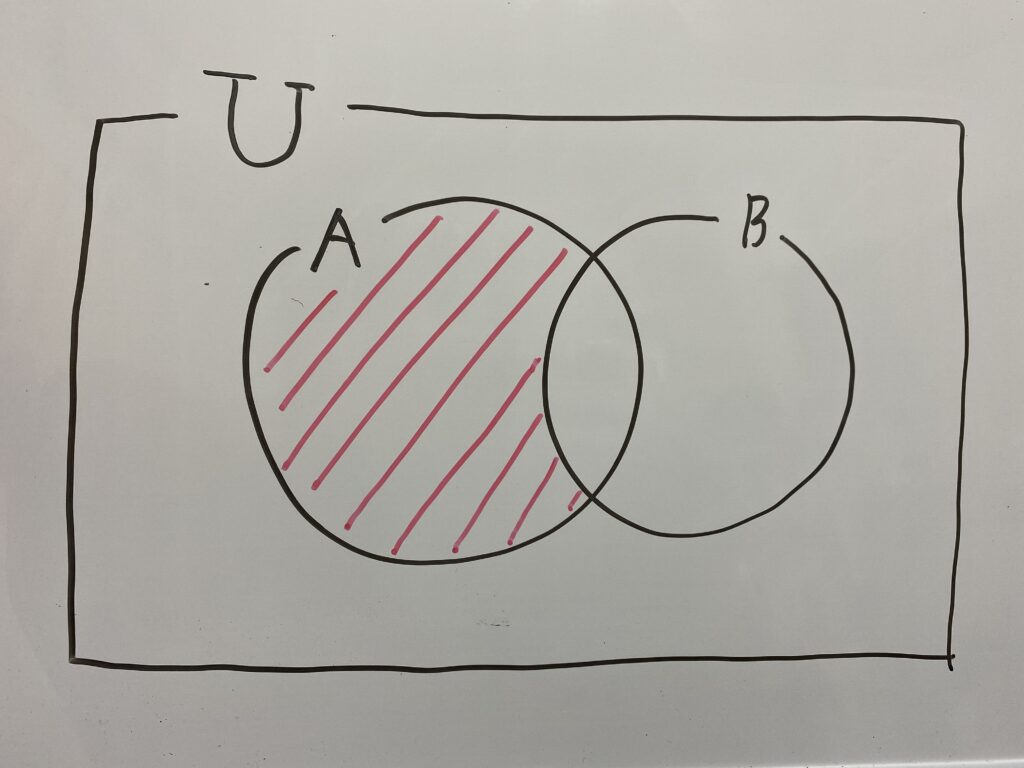
すると求めるには
$n(A)-n(A \cap B)$を計算すればいいことがわかりますね?
$n(A)=50$、$n(A \cap B)=16$をさきほど求めたため
$n(A)-n(A \cap B)=50-16=34$
答えは34
最後に
今回は要素の個数の求め方をしっかり解説しました。
・「ある範囲内での○の倍数の個数」の求め方

楽しい数学Lifeを!




