
みなさんこんにちは、ジルでございます!
さて今回は高校数学 数I『因数分解』の問題を実際に解いてみたいと思います。
ちなみにあまり得意ではない方向けに基礎をお話しした記事もありますのでよかったらご覧ください。

問題
(1)9x²−25y²
(2)2x²−24x+72
(3)18x²−21xy+6y²
(4)(x−3)²+3(x−3)−54
さあやっていきましょう。以前私が基礎の記事で書いた
①問題をじっくり眺める。
②共通項があれば、ab+ac=a(b+c)のようにしてまとめる。
③a²+2ab+b²=(a+b)²
a²−b²=(a+b)(a−b)
の公式が使えるかチェックする。使えれば使って、使えなければ④へ。
④acx²+(ad+bc)+bd=(ax+b)(cx+d) a,b,c,dは定数
を使って解く。
を基にしていきます。
解答
9x²−25y²
①問題をじっくり眺めましょう。
②共通項はなさそうですね。
③9x²−25y²=(3x)²−(5y)²
なので公式が使えます!したがって
9x²−25y²=(3x+5y)(3x−5y) 終
2x²−24x+72
①問題をじっくり眺めましょう。
②全部の項が2の倍数になっていますね?よって2が共通項です!したがって
2x²−24x+72=2(x²−12x+36)
あとはカッコの中を因数分解すればいいだけです。
③x²−12x+36=x²-2∙x∙6+6²
であることに注目します。公式が使えそうですね?したがって
2x²−24x+72=2(x²−12x+36)=2(x−6)² 終
18x²−21xy+6y²
①問題をじっくり眺めましょう。
②全ての項が3の倍数になっていますね?なので3が共通項です。したがって
18x²−21xy+6y²=3(6x²-7xy+2y²)
となります。これでカッコの中を因数分解すれば良くなりましたね!
③今回は公式は使えなさそうです。
④パッと見すぐには因数分解できなさそうです。よって「たすきがけ」を使います。

まだたすきがけが上手くできないそこのアナタ!
ひらすらたすきがけのやり方だけを書いた記事を作りましたのでよかったらご覧ください( ^ω^ )

上の記事でじっくりやり方を説明しましたので今回は少し省略型でやります。
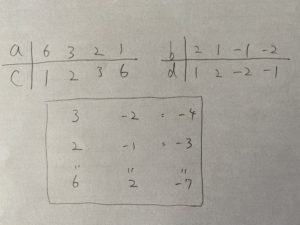
よって、
18x²−21xy+6y²=3(6x²−7xy+2y²)=3(3x−2y)(2x−y) 終
(x−3)²+3(x−3)−54
さてこちら、解き方は2つあります。
解き方1:全部展開してから因数分解する。
解き方2:『置き換え』を使う。

いつも言っていますが、因数分解の上達は解く数がモノを言います。
「置き換え」を利用する問題をたくさん解きましょう。
するとスピード・精度が向上します。
最後に
今回は4問だけ解きました。
口酸っぱくして言いますが、
たくさん問題をこなしましょう(● ˃̶͈̀ロ˂̶͈́)੭ꠥ⁾⁾
こなせばこなすほど上達しますから。
難しい問題編の解説記事も作る予定ですのでご覧くださいね!

ガンバ!



